摘要：为降低滤波系统和电网的参数变化对单独注入式有源电力滤波器(hybrid active power filter with single injection branch，SIBAPF)滤波性能的影响，提出了 SIBAPF 的模型参考自适应控制策略。建立了 SIBAPF 数学模型，并根据该模型建立了滤波系统参数自适应律。仿真结果表明，模型参考自适应控制方法较非线性 PI 控制方法滤波控制效果更好。基于该方法研制了 SIBAPF 试验样机，该样机投运后波效果良好，满足系统运行要求。
关键词：单独注入式有源电力滤波器；谐波治理；模型参考自适应控制
0 引言
随着电力电子器件在工业领域的广泛运用，谐波问题日益突出，目前谐波治理主要通过有无源滤波器、有源滤波器(active power filter，APF)以及各种混合型电力滤波器等[1-8]设备。文献[9]中单独注入式电力滤波器引入了基波谐振支路，减小了滤波器容量，增大了无功静止补偿能力，能够灵活应用于各种高低压滤波场合。

目前 APF 控制方法众多，如同步坐标系下的PI 控制法、广义积分法、单周控制法、预测控制法等[10-15]，该类方法控制效果较好，但其大多假定滤波系统与电网的参数恒定，忽略了滤波系统参数扰动的影响，具有一定的局限性。工程应用中滤波系统及电网的参数易受温度、磁场等外部环境的影响产生波动，同时元件老化等因素也易使滤波系统参数发生较大变化，而负载的改变也易将使电网参数发生变化，以上参数波动轻则影响滤波性能，重则将影响系统的安全运行。为此结合单独注入式滤波器的特点，本文提出了模型参考自适应控制(model referenced adaptive control，MRAC)方法，该方法能在被控对象参数未知且参数发生较大变化时，仍能使滤波系统维持在最优状态，改善滤波效果，以满足输配电系统高压大容量无功补偿和谐波治理的要求。

1 SIBAPF 系统建模
1.1 SIBAPF 结构
SIBAPF 主要由直流侧电容、逆变器、输出滤波电感、耦合变压器、基波串联谐振电路和注入电容组成，结构如图 1 所示。

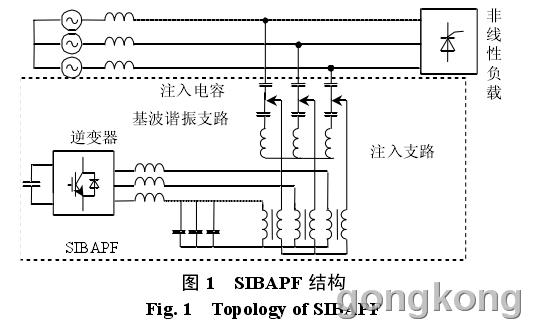
SIBAPF 在耦合变压器副边并联基波串联谐振电路，可减小逆变器容量。同时 SIBAPF 串入了无源滤波器，可提高整个系统的静止无功补偿能力。因此 SIBAPF 既能治理谐波，又能根据实际情况补偿无功功率。
SIBAPF 的控制主要通过逆变器实现，通常逆变器可以等效为电压源。滤波系统中存在大量的电感、电容等无源元件，无源元件的引入提高了系统阶数，增加了控制难度，控制器参数难以整定。另外，电网和滤波系统元件的参数存在时变性(如输出滤波器与基波谐振支路的电感间存在互感效应；电感电容等无源元件的内阻受温度影响较大，内阻变化会引起品质因数的变化；元件长时间使用易造成老化；电网负载是变化的)，元件参数的改变也增加了控制难度。
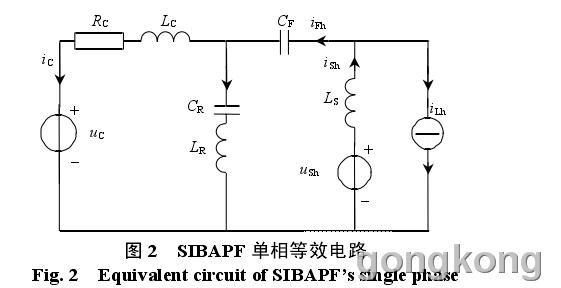
1.2 SIBAPF 模型
SIBAPF 在谐波域的单相等效电路如图 2 所示，其中，uSh为电网谐波电压，iLh为谐波源谐波电流，RC、LC分别为逆变器损耗、输出滤波器以及耦合变压器折算到变压器副边的等效阻抗的电阻和电感，iC为流入耦合变压器的电流，uC为折算到耦合变压器副边的逆变器输出电压，CR和 LR为基波谐振支路，LS为电网电感，Shi 为电网谐波电流，FC 为注入电，iFh为注入电容电流。
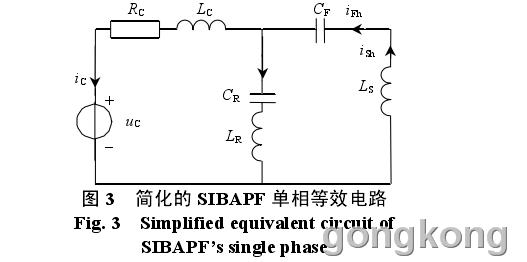
忽略系统阻抗，并假定电网为理想电压源，则将 SIBAPF 单相等效电路进行简化，如图 3 所示。
根据图 3 并利用回路分析法可求得 SIBAPF系统的时域电路方程：

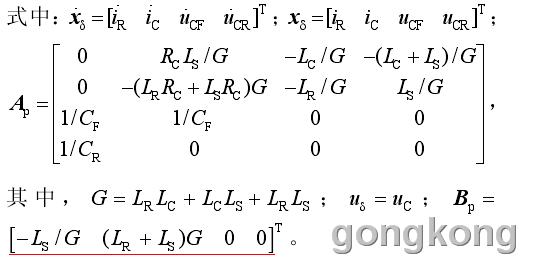
式(1)即为以被控对象状态方程形式表示的SIBAPF 的数学模型。矩阵 Ap、Bp相对自适应过程来说可以看成常数矩阵，模型以Cu 作为输入变量，通过控制Cu 来控制谐波源电流Ci ，该模型能直观体现输入变量与参数状态变量之间的关系。
2 MRAC 策略
文献[2]分析了注入式滤波器系统参数变化对滤波性能的影响，不同的滤波系统参数对滤波性能的影响不同(如 APF 中输出滤波器、基波谐振支路等元件参数的变化对滤波性能影响较为严重)，电网参数的变化对滤波器性能的影响相对较小。若采用常规控制策略，在滤波参数为已知定常数或变化很小可忽略时，SIBAPF 可以达到较为满意的控制效果。但滤波参数变化较大时，常规控制方式的控制效果将变差，因为参数变化会使本来处于最优状态的滤波系统变为不再最优甚至不稳定。
MRAC 系统[16-19]为非线性控制系统，系统本身、环境及干扰存在不确定性，该系统能实时修正结构参数，使系统处于最优状态。
MRAC 系统以系统参数作为变量，模型参数会随系统参数变化实时调整，并驱动系统跟踪参考模型状态，在线调整控制器参数。MRAC 原理如图 4
所示。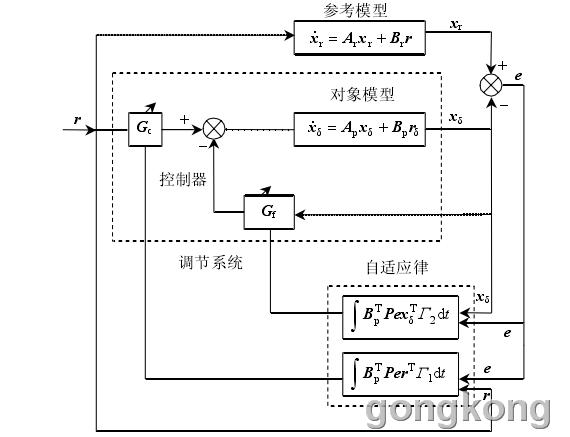

式中：Gc为前馈控制器增益矩阵；Gf为反馈控制器增益矩阵。将式(5)代入到式(2)可得

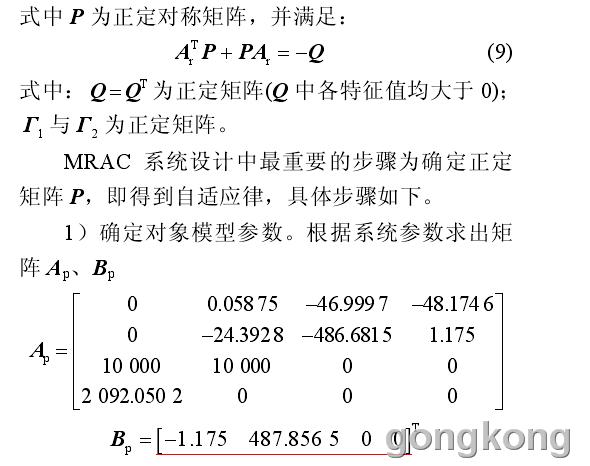
3 仿真验证
非线性 PI 控制方法能根据参数变化实时调整控制策略[22]，因此为验证本文方法的有效性，本节比较了非线性 PI 控制方法和本文方法的控制效果。电网电阻不变，0~0.9 s 电网电感为 0.05 mH，0.9 s 后电感跳变为 5 mH，各参数波形如图 5 所示。i_L为单相负载电流，i_S为电网电流，i_c为逆变器输出电流，error为电流误差。由图 5 可知，滤波系统参数未发生改变时，2 种控制方法能很好地满足滤波要求，但电感发生调整后，MRAC 方法在响应时间和滤波效果上均比非线性 PI 控制方法有优势。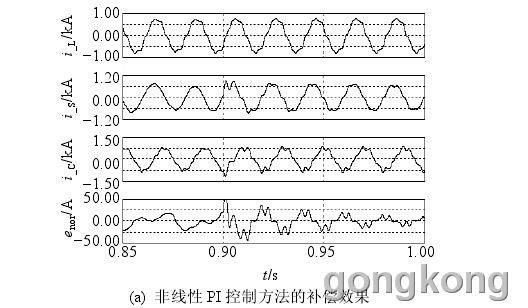
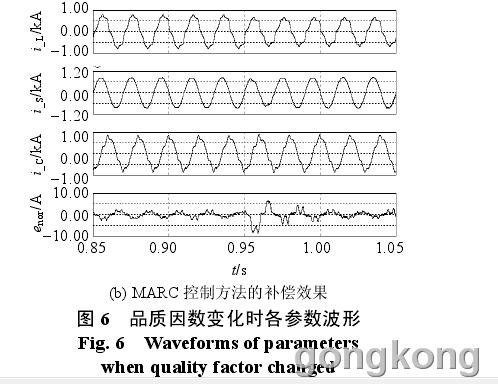
基波谐振支路品质因数 Q 变化时(0.9s 时 Q 由50 跳变为 40)，各参数波形如图 6 所示。由图 6 可知，Q 改变时，与非线性 PI 控制方法相比，MARC方法在控制精度以及调节速度上都有明显优势。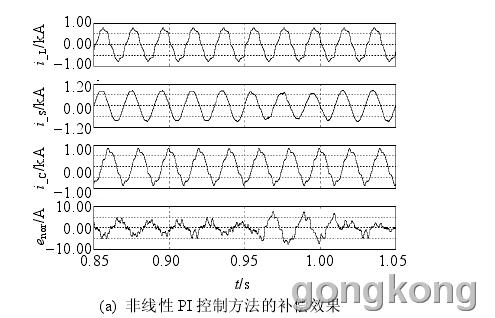

负载变化时，各参数波形如图 7 所示。电网负载初始时为非线性负载，0.9 s 时投入另一部分负载，其电阻、电抗分别为 5 、5mH。由图 7 可知，电网负载改变前后，2 种方法的滤波效果均较好，相对于非线性 PI 控制方法，MARC 方法响应速度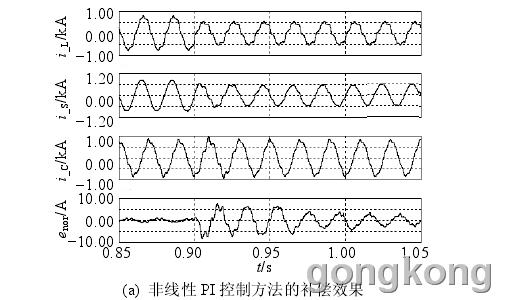

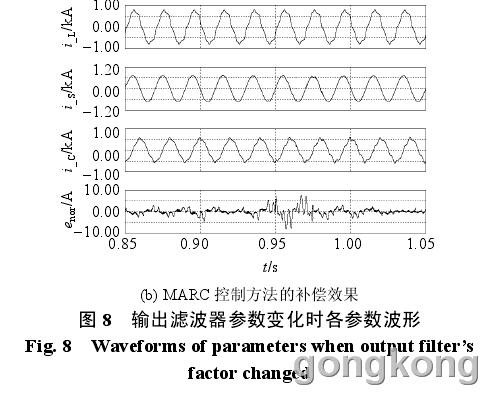
稍快。输出滤波器参数变化时(电感、电容初始值分别为 1 mH、60 μF，0.9 s 时电感增大为 2 mH)，各参数波形如图 8 所示。由图 8 可知，非线性 PI 控制方法在滤波器参数改变前滤波效果均好，但滤波器参
数改变后滤波性能明显降低，毛刺增加，波形畸变；而 MARC 方法经过短时间调整后能够有效滤除电网谐波。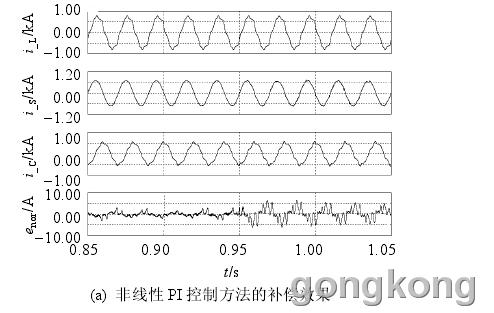

由以上分析可知，影响系统滤波效果的主要参数为负载以及输出滤波器参数，而电网参数和基波谐振支路参数对滤波性能影响不大，且 MARC 方法总体性能明显优于非线性 PI 控制方法。但本文仿真没有考虑逆变器容量限制问题，没有分析基波谐振支路参数变化导致逆变器容量加大等问题，今后应对其进行进一步研究。
4 样机试验
本文研制了采用MRAC方法的SIBAPF试验样机。非线性负荷由可控整流电路模拟，逆变器采用三菱公司生产的智能功率模块 PM300DSA120，其额定电压为 1.2 kV，额定电流为 300 A，直流侧电流为 380 V。图 9 为 SIBAPF 投运前后的参数波形。由图9可知，滤波装置投运前，电网电流畸变严重，5、7、11、13 次谐波的畸变率分别为 22.3%、17.2%、9.4%和 7.5%；SIBAPF 投运后电流畸变率下降为 2.35%、1.22%、2.75% 和 1.67%，滤波效果显著。同时系统对无功功率进行了补偿，功率因数由 0.78 上升到0.95。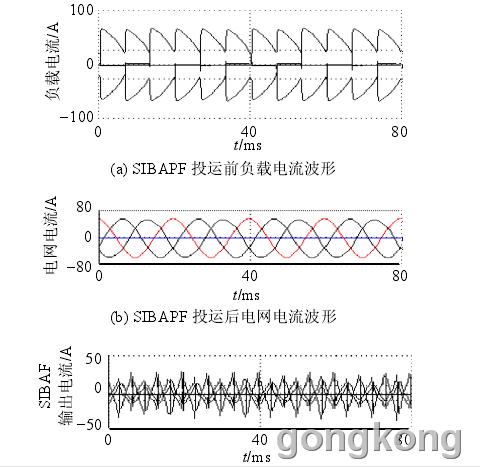

(c) SIBAPF 输出电流波形
图 9 样机试验波形
Fig. 9 Waveforms of test prototype
5 结论
本文方法兼顾了谐波治理和无功补偿，能根据自适应律对模型参数进行最优调整，使滤波系统始终维持在最优状态，适用能力强，动态响应性能良好。但基波谐振支路参数变化可能导致一部分基波电流流入到逆变器，从而增加逆变器容量，尤其当基波电流过大时将严重威胁滤波系统的安全稳定运行，因此今后应进一步研究基波电流对滤波系统的影响。参考文献
[1] 王兆安，杨君，刘进军．谐波抑制与无功补偿[M]．北京：机械工业出版社，1998：328-332．
[2] 罗安．电网谐波治理和无功补偿技术及装备[M]．北京：中国电力出版社，2006：7-12，125-136．
[3] Senini S，Wolfs P J．Analysis and design of a multiple loop control system for a hybrid active filter[J] ． IEEE Trans on Industrial Electronics，2002，49(6)：1283-1292．
[4] Currence E J，Plizga J E ，Nelson J P．Harmonic resonance at a medium-sized industrial plant[J] ． IEEE Trans on Industry Applications，1995，31(4)：682-690．
[5] Detjen D，Jacobs J，De Doncker R W，et al．A new hybrid filter to dampen resonances and compensate harmonic currents in industrial power systems with power factor correction equipment[J]．IEEE Trans on Power Electronics，2001，16(6)：821-827．